Mạch Song Song【The Parallel Circuit】
Mạch song song là khi các điện trở không được kết nối từ đầu đến đuôi liên tiếp như mạch nối tiếp, mà thay vào đó chúng được kết nối song song với nhau. Điều này có nghĩa là có nhiều đường dẫn khác nhau cho dòng điện chảy qua.
Ví dụ, khi hai ổ cắm đèn được kết nối bằng hai dây từ cực này đến cực kia, chúng tạo thành một mạch song song. Khi kết nối bất kỳ cặp cực nào qua nguồn điện, tất cả các thành phần – đèn, nguồn điện và dây kết nối – tạo thành một mạch song song hoàn chỉnh.
Tương tự, khi các ô pin (tế bào pin | cell) trong một bộ pin (battery) được kết nối để có nhiều đường dẫn cho dòng điện, chúng được gọi là kết nối song song. Mỗi ô pin (cell) chỉ cung cấp một phần của tổng dòng điện lấy từ bộ pin (battery). Khi kết nối các ô pin (cell) song song, bạn phải kết nối cực dương của chúng với nhau và cực âm của chúng với nhau.
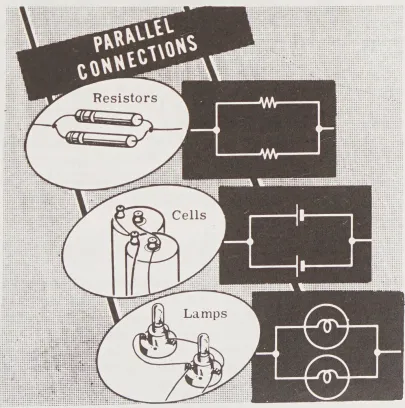
Một ví dụ rõ ràng về kết nối song song được tìm thấy trong hệ thống dây điện của một ngôi nhà thông thường, trong đó mọi thiết bị điện sử dụng trong nhà đều được kết nối song song qua dây nguồn.
Điện Áp Trong Mạch Song Song【Voltage in Parallel Circuits】
Trong mạch song song, khi các điện trở được kết nối qua một nguồn điện áp (voltage source), điện áp (voltage) qua mỗi điện trở luôn là như nhau. Nhưng lưu lượng dòng điện (current) qua mỗi điện trở sẽ biến đổi tùy thuộc vào giá trị của từng điện trở.
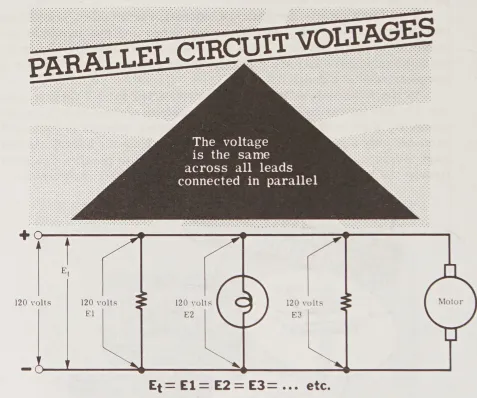
Chú Thích
- (Parallel circuit voltages): Điện áp trong Mạch Song Song
- (The voltage is the same across all leads connected in parallel): Điện áp là giống nhau trên tất cả các dây dẫn được kết nối song song
Trong mạch song song, việc mỗi điện trở hoặc tải nhận cùng một điện áp có tác động quan trọng trong thực tế. Để hoạt động bình thường đúng cách, tất cả các thành phần được kết nối song song phải có cùng mức điện áp.
Ở Hoa Kỳ, điện áp tiêu chuẩn trên dây là 120 volt. Bạn có thể đã biết rằng đèn và các thiết bị điện khác với điện áp đánh giá đánh giá là 120 volt hoặc gần đó sẽ hoạt động tốt. Ngược lại, bóng đèn có điện áp định mức đánh giá là 12 volt sẽ cháy hỏng ngay lập tức vì dòng điện quá lớn. Lý do là vì tất cả các thiết bị đều được kết nối vào cùng một nguồn điện áp, nên mỗi thiết bị đều nhận cùng một điện áp. Do đó, tất cả phải có điện áp định mức phù hợp để xử lý điện áp này.
Dòng Điện Trong Mạch Song Song【Current Flow in Parallel Circuits】
Dòng điện chảy qua một mạch song song sẽ chia ra để đi qua mỗi đường song song. Lấy ví dụ một mạch bao gồm ba nhánh – gọi là AB, CD, và EF, mỗi nhánh được kết nối song song với nhau. Trong một mạch như vậy:
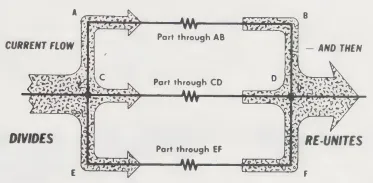
Chú Thích
- (Current flow): Dòng Điện
- (Divides): Phân chia (tách ra)
- (Part through AB, CD EF): Một phần qua AB, một phần qua CD, một phần qua EF
- (And then, re-unites): Sau đó, hợp lại
Trong mạch song song, dòng điện chia theo tỷ lệ nghịch, phụ thuộc vào điện trở của từng nhánh riêng lẻ. Điều này có nghĩa là những nhánh có điện trở thấp hơn so với các nhánh khác trong cùng một mạch sẽ thu hút nhiều dòng điện hơn. Để nói một cách đơn giản và chính xác, trong mạch điện song song, các nhánh có điện trở thấp sẽ thu hút nhiều dòng điện hơn so với các nhánh có điện trở cao.
Trong hình minh họa bên dưới, các giá trị khác nhau của bốn điện trở trong mạch song song được biểu thị bằng độ dài của ký hiệu điện trở được sử dụng trong mỗi trường hợp. Lưu ý rằng điện trở càng cao thì tỷ lệ dòng điện chạy qua nó càng nhỏ và ngược lại.
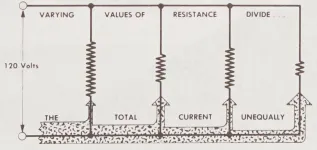
Chú Thích
- (Varying values of resistance divide, the total current unequally): Các giá trị điện trở khác nhau sẽ chia dòng điện tổng một cách không đồng đều
Cách dòng điện chia ra trong mạch song song rất quan trọng trong thực tế. Ví dụ, vì mọi thiết bị điện trong nhà (như bạn đã biết) được kết nối song song trên dây điện, dòng điện sẽ chia ra không đồng đều qua các thiết bị có điện trở khác nhau, với dòng điện lớn nhất sẽ chảy qua điện trở có điện trở thấp nhất. Bạn sẽ hiểu cách ngăn chặn dòng điện quá mức khi tìm hiểu về cầu chì sau này.
Hãy nhớ lại những điều quan trọng mà bạn vừa học. Khi kết nối các điện trở không bằng nhau song song, khả năng chống lại dòng điện không đồng đều trong từng nhánh của mạch. Điện trở nhỏ hơn tạo ra ít sự chống lại dòng điện hơn. Dòng điện luôn chảy mạnh nhất qua con đường có ít sự chống lại nhất; do đó, các điện trở nhỏ trong mạch song song luôn cho dòng điện qua nhiều hơn so với các điện trở lớn hơn.
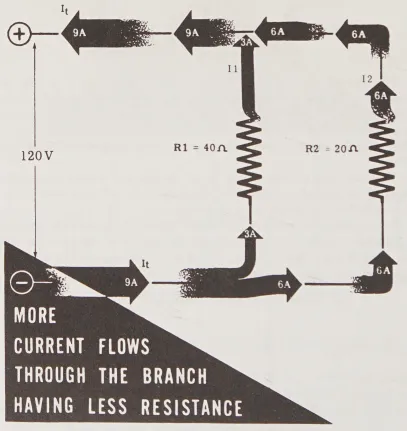
Ví dụ, trong mạch dưới đây, tổng cộng 9 ampe chảy qua một mạch song song gồm hai điện trở R1 và R2, trong đó R1 có giá trị gấp đôi R2.
Chú Thích
- (More current flows through the branch having less resistance): Dòng điện nhiều hơn sẽ chảy qua nhánh có điện trở ít hơn
Chú ý rằng dòng điện chia tỷ lệ nghịch với giá trị của hai điện trở – chỉ có 3 ampe chảy qua điện trở 40 ohm của R1, trong khi có 6 ampe chảy qua điện trở 20 ohm của R2. Nếu giá trị của R1 tăng lên gấp bốn lần thành 160 ohm, thì dòng điện qua R1 sẽ giảm từ 3 ampe xuống còn 3/4 ampe, trong khi dòng điện qua R2 không thay đổi. Vì vậy, tổng dòng điện sẽ là: 6 ampe cộng với 3/4 ampe, tức là 6,75 ampe.
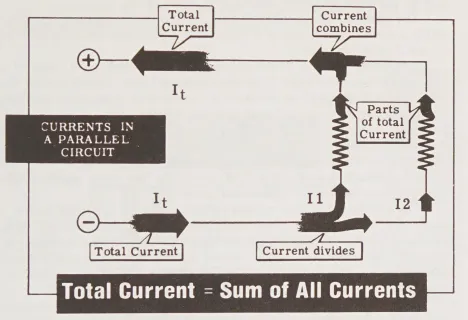
Bạn có thể đã nhận thấy trên trang trước rằng tổng dòng điện trong một mạch song song dường như bằng tổng của dòng điện trong từng thành phần. Điều này luôn đúng và có thể được diễn đạt như sau: Tổng dòng điện trong mạch bằng tổng của dòng điện qua mỗi thành phần ” I_{t} = I_{1} + I_{2} + I_{3} + … “.
Chú Thích
- (Currents in a parallel circuit): Dòng điện trong một mạch song song
- (Total current): Tổng dòng điện
- (Current divides): Dòng điện được chia ra
- (Parts of total current): Một phần của dòng điện tổng
- (Current combines): Dòng điện kết hợp lại
- (Total Current = Sum of All Currents): Tổng dòng điện = Tổng của tất cả các dòng điện trong mạch
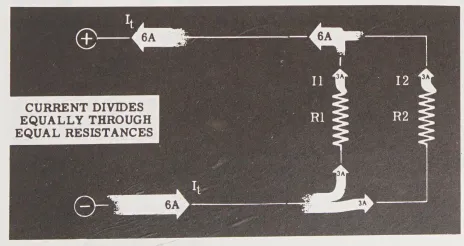
Khi một mạch có các điện trở bằng nhau và mắc song song, dòng điện chảy qua mỗi điện trở sẽ bằng nhau; và dòng điện, luôn chọn đường có ít lực cản nhất, sẽ gặp sự kháng cự như nhau trên mọi con đường có thể đi.
Chú Thích
- (Current divides equally through equal resistances): Dòng điện chia đều qua các điện trở có cùng giá trị
Các Điện Trở Bằng Nhau Trong Mạch Song Song【Equal Resistors in Parallel Circuits】
Trong mạch điện giống như hình ở minh họa, dòng điện chạy qua mỗi điện trở đều bằng nhau. Điều này xảy ra bởi dòng điện chia đều từ tổng dòng điện sang số lượng điện trở mắc song song. Luật này áp dụng cho bất kỳ số lượng điện trở nào, miễn là chúng có cùng giá trị.
Tiếp theo là tính tổng điện trở hiệu dụng của mạch gồm nhiều điện trở bằng nhau. Bạn biết rằng, diện tích mặt cắt ngang của một điện trở tăng lên sẽ giảm điện trở. Điều này giống như khi kết nối nhiều điện trở song song, tạo ra một diện tích lớn hơn cho dòng điện chảy qua, dẫn đến việc dòng điện lưu thông dễ dàng hơn.
Bạn có thể hiểu điều này như việc có hai ống nước song song trong hệ thống. Dưới áp lực nước không đổi, hai ống này cùng nhau sẽ truyền lượng nước lớn hơn so với mỗi ống riêng lẻ.
Tóm lại, khi kết nối các điện trở hoặc tải song song, tổ hợp này có điện trở hoặc tải kết hợp thấp hơn so với mỗi cái riêng lẻ. Ví dụ, nếu bạn có bốn điện trở 200 ohm mắc song song, tổng điện trở của chúng sẽ chỉ bằng 1/4 giá trị của mỗi điện trở.
Như vậy, tổng điện trở sẽ là 50 ohm; và kết nối song song này sẽ tương đương với một điện trở duy nhất có giá trị 50 ohm. Khi tính toán, việc kết hợp các tải song song thành một tải duy nhất sẽ thuận tiện hơn.

Chú Thích
(Finding Resistance Of Equal Resistors In Parallel): Tìm điện trở của các điện trở bằng nhau trong kết nối song song
Các Điện trở Không Bằng Nhau Trong Mạch Song Song【Unequal Resistors in Parallel Circuits】
Khi có các điện trở không giống nhau mắc song song trong mạch, việc tính tổng điện trở trở nên phức tạp hơn.
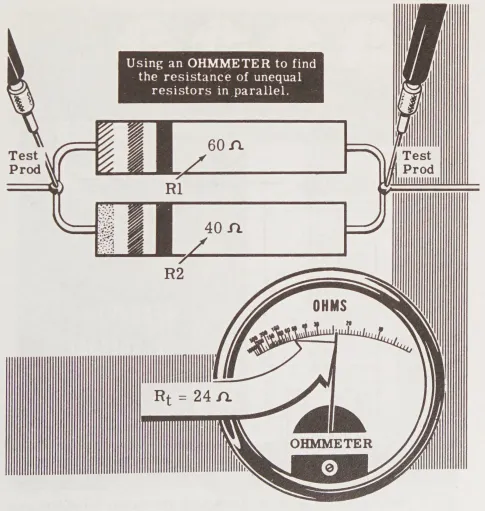
Trong một trường hợp thuận lợi, bạn có thể sử dụng một bộ đo ohm kế để tìm ra giá trị tương đương của tổng điện trở từ hai điện trở không giống nhau mắc song song. Ví dụ, trong một mạch song song với hai điện trở, R1 và R2, có giá trị lần lượt là 60 và 40 ohm, bạn sẽ đo được tổng điện trở là 24 ohm.
Chú Thích
- (Using an ohmmeter to find the resistance of unequal resistors in parallel): Dùng ôm kế để đo điện trở của các điện trở không giống nhau khi chúng được nối song song
Thí Nghiệm/Ứng Dụng – Điện Áp Trong Mạch Song Song【Experiment/Application-Parallel Circuit Voltage】
Trong mạch song song, mặc dù dòng điện qua các nhánh không luôn giống nhau, nhưng điện áp trên mỗi nhánh đều bằng nhau. Khi bạn kết nối ba ổ cắm đèn song song và lắp đèn 6 volt, 250 mA (0,25 ampe) vào mỗi ổ cắm, bạn sẽ thấy rằng mỗi đèn sáng với độ sáng như nhau như khi chỉ có một đèn duy nhất, và cho ba đèn, dòng điện trong mạch là 750 mA. Ngoài ra, giá trị vôn kế qua cực của pin vẫn như nhau cho dù sử dụng một, hai hay ba đèn.

Chú Thích
- (Measuring the voltage in a parallel circuit): Đo điện áp trong một mạch song song
Nếu bạn tháo dây đo điện áp từ cực của pin, và kết nối dây đo điện áp qua các cực của mỗi ổ cắm đèn một cách lần lượt, bạn sẽ thấy rằng điện áp là như nhau qua mỗi chiếc đèn và bằng với điện áp của nguồn pin. Điều này chứng tỏ rằng điện áp qua mỗi thành phần mạch là như nhau trong một mạch song song.
Thí nghiệm/Ứng dụng – Dòng Điện Trong Mạch Song Song【Experiment/Application-Parallel Circuit Current】
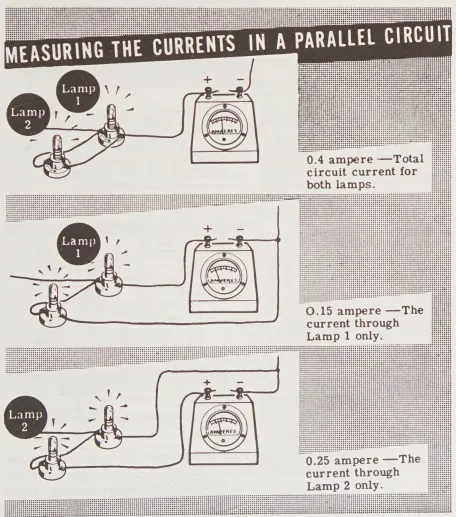
Để minh họa việc chia dòng điện, bạn có thể thay thế bóng đèn 250 mA bằng bóng đèn 150 mA như được minh họa. Bằng cách nối ampe kế lần lượt với một đèn, sau đó với đèn khác, bạn sẽ thấy rằng tổng dòng điện 400 mA được phân chia, với 250 mA chảy qua một đèn và 150 mA chảy qua đèn kia. Sau đó, kết nối ampe kế để đọc tổng dòng điện ở đầu kết hợp song song đối diện với đầu mà nó được kết nối ban đầu. Bạn sẽ thấy rằng tổng dòng điện ở mỗi đầu của mạch song song là như nhau, dòng điện chia ra chạy qua các nhánh song song của mạch và kết hợp lại sau khi đi qua các nhánh này.
Chú Thích
- (Measuring the currents in a parallel circuit): Đo dòng điện trong mạch song song
- (0.4 ampere-Total circuit current for both lamps): 0,4 ampere – Tổng dòng điện của cả hai bóng đèn
- (0.15 ampere-The current through Lamp 1 only.): 0,15 ampere – Dòng điện chỉ qua Bóng đèn 1
- (0.25 ampere-The current through Lamp 2 only): 0,25 ampere – Dòng điện chỉ qua Đèn 2
Thí nghiệm/Ứng dụng – Điện Trở Trong Mạch Song Song【Experiment/Application-Parallel Circuit Resistance】
Khi tổng dòng điện trong mạch tăng mà điện áp không đổi, tổng điện trở sẽ giảm. Để minh họa điều này, hãy kết nối hai ổ cắm đèn mắc song song. Điều này được thực hiện bằng cách nối chúng qua các cực của một pin 6 volt và sử dụng một ampe kế để đo tổng dòng điện. Khi một vôn kế được kết nối qua các cực của pin, bạn sẽ thấy điện áp vẫn là 6 volt. Khi chỉ có một đèn 250 mA, 6 volt được kết nối, ampe kế chỉ ra dòng điện khoảng 250 mA và vôn kế chỉ ra 6 volt. Khi cả hai đèn được lắp kết nối, giá trị dòng điện tăng lên 500 mA (0,5 ampere), nhưng điện áp vẫn ở mức 6 volt, cho thấy mạch song song có điện trở nhỏ hơn so với việc sử dụng đèn đơn.

Chú Thích
- (How parallel connections reduce resistance): Làm thế nào Kết nối song song giảm điện trở
- (Single lamp inserted): Đèn đơn được cắm vào
- (Both lamps inserted – current increases): Cả hai bóng đèn được cắm vào – dòng điện tăng
Khi lần lượt cắm từng bóng đèn vào, bạn sẽ thấy rằng dòng điện đo được trên ampe kế cho mỗi bóng đèn là 250 mA; nhưng khi cả hai bóng đèn được cắm vào, tổng dòng điện đo được là 500 mA. Điều này chỉ ra rằng dòng điện tổng là 500 mA được chia thành hai dòng điện 250 mA, mỗi dòng điện này chảy qua một bóng đèn hoặc một con đường riêng biệt.
Thí Nghiệm/Ứng dụng – Các Điện Trở Song Song【Experiment/Application-Parallel Resistances】
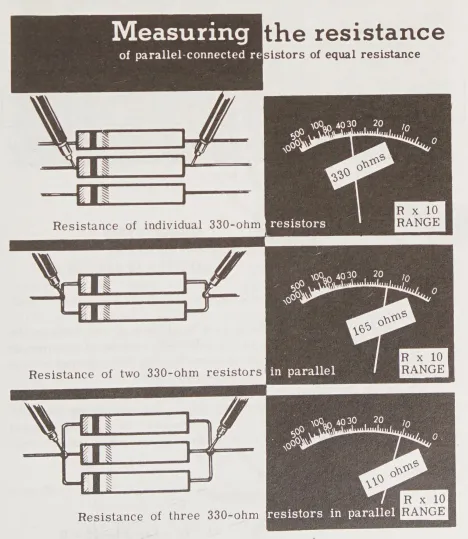
Để cho thấy làm thế nào việc kết nối điện trở song song giảm điện trở tổng, bạn có thể đo điện trở của ba điện trở 330 ohm một cách riêng lẻ bằng bộ đo ohm kế. Khi hai trong số ba điện trở 330 ohm được kết nối song song, điện trở tổng nên là 165 ohm; điều này được thể hiện bằng cách kết nối chúng và đo điện trở song song bằng bộ đo ohm kế. Khi một điện trở 330 ohm khác được kết nối song song, bạn sẽ thấy rằng điện trở giảm xuống một giá trị là 110 ohm. Điều này không chỉ cho thấy rằng kết nối các điện trở bằng nhau song song giảm điện trở tổng, mà còn cho thấy rằng điện trở tổng có thể được tìm thấy bằng cách chia giá trị của một điện trở đơn lẻ cho số lượng điện trở được sử dụng.
Chú Thích
- (Measuring the resistance of parallel-connected resistors of equal resistance): Đo điện trở của các điện trở được kết nối song song có cùng giá trị điện trở
- (Resistance of individual 330-ohm resistors): Điện trở của các điện trở đơn lẻ có giá trị 330 ohm
- (Resistance of two 330-ohm resistors in parallel): Điện trở của hai điện trở 330 ohm được kết nối song song
- (Resistance of three 330-ohm resistors in parallel): Điện trở của ba điện trở 330 ohm được kết nối song song
Định Luật Đầu Tiên Của Kirchhoff【Kirchhoff’s First Law】
Thường không thể sử dụng một bộ đo ohm để đo điện trở – và trong mọi trường hợp, bạn nên biết cách tìm các giá trị như vậy thông qua phép tính. Bạn sẽ không ngạc nhiên khi nghe rằng việc này dễ dàng thực hiện thông qua việc sử dụng sáng suốt Định luật Ohm – nhưng bạn cũng sẽ cần sự giúp đỡ từ một phương trình khác mà bạn đã chờ đợi một thời gian để nghe về. Nó được biết đến với tên gọi là Định luật đầu tiên của Kirchhoff.
Bạn đã biết rằng trong một mạch nối tiếp, dòng điện đi vào mạch chính bằng chính dòng điện ra khỏi mạch đó. Nếu bạn đã hiểu ý tưởng về dòng điện như một luồng electron di chuyển trong mạch, bạn sẽ thấy rằng điều này phải đúng, bất kể mạch đó là nối tiếp, song song, hoặc bất kỳ sự kết hợp nào của hai loại mạch đó.
Vậy nên, Luật đầu tiên của Kirchhoff áp dụng cho mọi loại mạch. Tuy nhiên, nó không áp dụng cho toàn bộ mạch, mà chỉ liên quan đến các điểm nối riêng lẻ trong mạch, nơi các dòng điện kết hợp với nhau. Luật nói rằng: Tổng của tất cả các dòng điện chảy vào một nút (một điểm nối) luôn bằng tổng của tất cả các dòng điện chảy ra khỏi nút (điểm nối) đó.
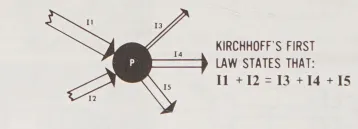
Hãy tưởng tượng bạn có một mạch điện, trong đó có một điểm nối gồm năm dây dẫn và tất cả năm dây đều mang dòng điện theo các hướng như minh họa dưới đây.
Chú Thích
- (Kirchhoff’s first law states that: I_{1} + I_{2} = I_{3} + I_{4} + I_{5}): Luật thứ nhất của Kirchhoff nói rằng: Tổng dòng điện vào một điểm nối bằng tổng dòng điện ra khỏi điểm đó I_{1} + I_{2} = I_{3} + I_{4} + I_{5}
Sự thật về Định luật thứ nhất của Kirchhoff là rõ ràng nếu bạn nhìn vào hình vẽ . Các dòng điện I_{1} và I_{2} đang mang theo luồng electron đến Điểm P. Do đó, số lượng electron rời khỏi Điểm P luôn phải bằng số lượng electron đến đó.
Lưu ý điểm quan trọng là hướng đã được gán cho dòng điện. Dù bạn sử dụng dòng chảy điện truyền thống (conventional current flow) hay dòng chảy electron (electron-current flow), hướng không quan trọng miễn là bạn nhất quán. Trong trường hợp này, dòng điện vào nút (điểm nối) được gán là dương, và dòng điện chảy ra là âm.
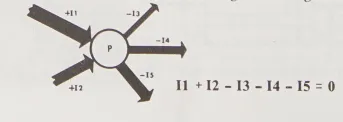
Để sử dụng Định luật thứ nhất của Kirchhoff trong một mạch hoàn chỉnh, quy tắc là (như luôn luôn): Đầu tiên vẽ mạch điện. Sau đó chỉ ra trên sơ đồ mạch hướng dòng điện chảy qua mỗi điện trở trong mạch. Tiếp theo, xác định xem trong số các dòng này, dòng nào chảy vào và dòng nào chảy ra khỏi mỗi điểm nối trong mạch. Đánh dấu thông tin này trên sơ đồ mạch. Giá trị và hướng dòng của các dòng chưa biết thường có thể được xác định bằng cách áp dụng Định luật. Tại điểm nối mạch như hình dưới đây, không biết hướng hoặc giá trị của I_{1}.
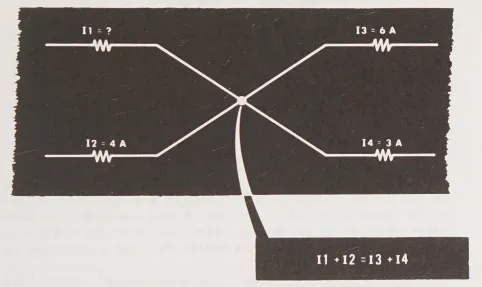
Hướng của dòng điện chưa biết được xác định bằng cách tổng hợp tất cả các dòng điện đã biết chảy vào và chảy ra khỏi điểm nối, rồi so sánh hai tổng này. Ở đây, tổng của các dòng điện chảy ra khỏi điểm nối (I_{3} = 6 ampe + I_{4} = 3 ampe, tổng cộng là 9 ampe) lớn hơn giá trị của dòng điện đã biết (I_{2} = 4 ampe) chảy vào điểm nối.
Do đó, dòng điện chưa biết (I_{1}) cũng phải chảy vào điểm nối, nếu không sẽ không thể duy trì cân bằng dòng electron tại điểm nối được. Giá trị của nó có thể được xác định bằng cách sử dụng phương trình Kirchhoff, I_{1} + I_{2} = I_{3} + I_{4}.
Do đó, I_{1} + 4A = 6A + 3A = 9A
I_{1} = 9A – 4A = 5A
Cũng sử dụng I_{1} + I_{2} – I_{3} – I_{4} = 0
I_{1} + 4A – 6A – 3A = 0
I_{1} – 5A = 0
I = 5A.
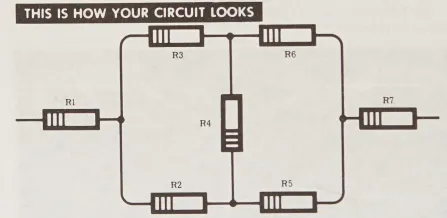
Giờ hãy xem một ví dụ phức tạp hơn về việc sử dụng Định luật thứ nhất của Kirchhoff để tìm ra các giá trị và hướng dòng điện chưa biết trong một mạch điện. Giả sử bạn có một mạch điện gồm bảy điện trở, được kết nối như hình dưới đây. Đây là một mạch vừa nối tiếp – vừa song song (series-parallel circuit), một loại mạch mà bạn sẽ học thêm nhiều sau này.
Chú Thích
- (This is how your circuit looks): Đây là dạng mạch của bạn
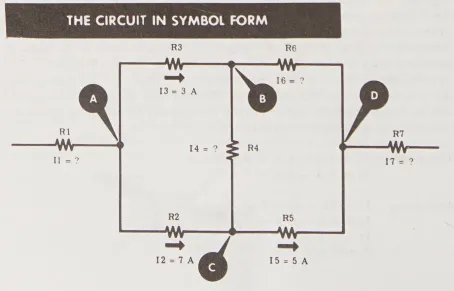
Bạn biết rằng dòng điện qua R_{2} là 7 ampe chảy vào phía R_{5}; dòng điện qua R_{3} là 3 ampe chảy vào phía R_{6}; và dòng điện qua R_{5} là 5 ampe chảy vào phía R_{7}. Tuy nhiên, bạn không biết gì về dòng điện qua các điện trở R_{1}, R_{4}, R_{6}, và R_{7}; nhưng bạn cần phải biết cả giá trị và hướng dòng điện của chúng. Dưới đây là cách làm.
Bắt đầu vẽ mạch theo dạng ký hiệu, chỉ rõ tất cả các dòng điện, kèm giá trị và hướng nếu đã biết. Tiếp theo, xác định từng điểm nối của hai hoặc nhiều điện trở bằng cách đặt một chữ cái.
Chú Thích
- (The circuit in symbol form): Mạch trong dạng ký hiệu biểu tượng
Tìm dòng điện chưa biết ở tất cả các điểm nối chỉ có một dòng điện chưa biết; sau đó, bạn có thể sử dụng các giá trị mới này để tìm các giá trị chưa biết ở các điểm nối khác. Trong mạch, bạn có thể thấy rằng các điểm nối A và C chỉ có một dòng điện chưa biết. Vì vậy, bắt đầu bằng cách tìm dòng điện chưa biết tại điểm nối A:
Trong ba dòng điện tại điểm nối A – I_{1}, I_{2} và I_{3} – cả I_{2} và I_{3} đều đã biết và chảy ra khỏi điểm nối. Vì vậy, dòng I_{1} phải chảy vào điểm nối, và giá trị của nó phải bằng tổng của I_{2} và I_{3}.
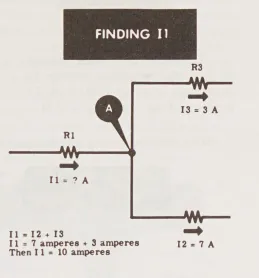
Tiếp theo, tìm dòng điện chưa biết tại điểm nối C.
Ở điểm nối C, có hai dòng điện đã biết – I_{2} và I_{5} – và chỉ có I_{4} là chưa biết. Vì I_{2}, chảy vào C, lớn hơn I_{5}, chảy ra khỏi C, nên dòng điện thứ ba I_{4} cũng phải chảy ra khỏi C. Ngoài ra, vì tổng dòng điện chảy vào C bằng với tổng dòng điện chảy ra khỏi nó, nên I_{2} bằng tổng của I_{4} và I_{5}.
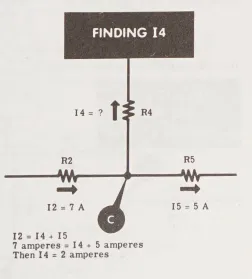
Bây giờ khi đã biết giá trị và hướng của I_{4}, chỉ còn I_{6} là chưa biết tại điểm nối B. Bạn có thể tìm giá trị và hướng của I_{6} bằng cách áp dụng định luật về dòng điện tại B.
Cả I_{3} và I_{4} đều chảy vào B; do đó, dòng điện còn lại I_{6} phải chảy ra khỏi B. Ngoài ra, I_{6} phải bằng tổng của I_{3} và I_{4}.
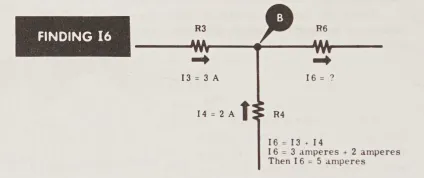
Với I_{6} đã biết, chỉ còn I_{7} là chưa biết, tại điểm nối D.
Vì I_{5} và I_{6} đều chảy vào điểm nối D, dòng điện I_{7} phải chảy ra khỏi D và bằng tổng của I_{5} và I_{6}.
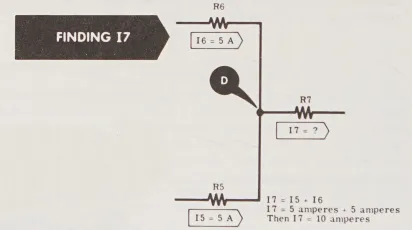
Bây giờ bạn đã biết tất cả các dòng điện trong mạch và hướng chảy của chúng qua các điện trở khác nhau.
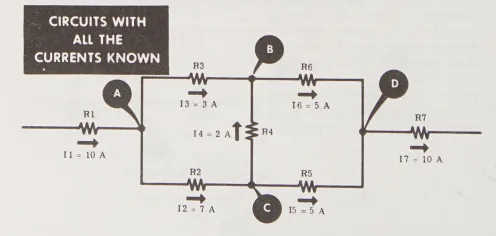
Chú Thích
- (Circuits with all the currents known): Mạch với tất cả các dòng điện đã biết.
Thí Nghiệm/Ứng Dụng – Định Luật Đầu Tiên Của Kirchhoff【Experiment/Application- Kirchhoff’s First Law】
Hãy tự kiểm tra Định luật đầu tiên của Kirchhoff – định luật về dòng điện trong mạch. Giả sử bạn kết nối một điện trở 15 ohm nối tiếp với một kết hợp song song của ba điện trở 15 ohm, sau đó kết nối toàn bộ mạch qua một viên pin khô 9 volt với một công tắc và một cầu chì nối tiếp.
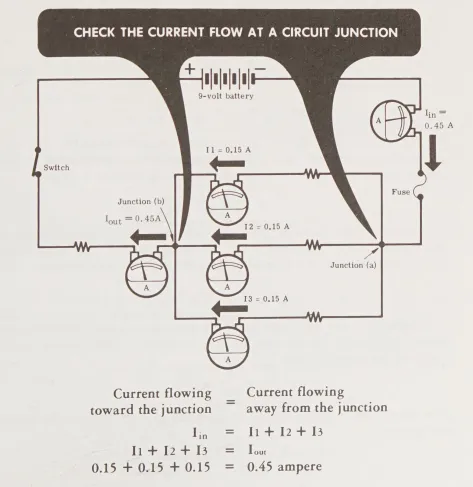
Tổng trở kháng (điện trở) của mạch là 20 ohm, dẫn đến một dòng điện tổng mạch là 0.45 ampe. Dòng điện này phải chảy qua mạch từ cực âm (-) đến cực dương (+) của pin (xem sơ đồ mạch bên dưới). Tại điểm nối (a), dòng điện mạch – 0.45 ampe – chia ra để chảy qua ba điện trở song song vào điểm nối (b). Vì các điện trở song song đều bằng nhau, dòng điện chia đều, mỗi điện trở chảy 0.15 ampe. Tại điểm nối (b), ba dòng điện song song kết hợp lại, chảy ra khỏi mạch qua điện trở nối tiếp.
Nếu bạn kết nối một ampe kế để đọc dòng điện trong mỗi dây dẫn tại điểm nối (b), bạn sẽ thấy tổng của ba dòng điện chảy vào điểm nối bằng với dòng điện chảy ra khỏi điểm nối.
Chú Thích
- (Check the current flow at a circuit juntion): Kiểm tra dòng điện tại một điểm nối trong mạch điện
- (Current flowing toward the junction = Current flowing away from the junction): Dòng điện chảy vào điểm nối = Dòng điện chảy ra khỏi điểm nối
Các Điện trở Không Bằng Nhau Trong Mạch Song Song (Tiếp Theo)【Unequal Resistors in Parallel Circuits】
Với hiểu biết về định luật thứ nhất của Kirchhoff, bạn đã sẵn sàng để quay lại chủ đề về các điện trở không bằng nhau trong mạch song song và tìm hiểu cách tính điện trở hiệu dụng của bất kỳ số lượng điện trở không bằng nhau nào được kết nối song song.
Trong mạch điện như hình minh họa, dòng điện chia thành ba phần để đi qua ba điện trở. Hãy áp dụng Định luật đầu tiên của Kirchhoff và Định luật Ohm vào mạch điện giống như bạn đã làm trước đó.
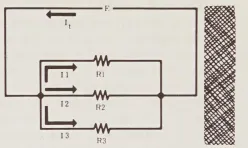
Bạn biết từ Định luật đầu tiên của Kirchhoff rằng, trong một mạch như mạch trên, (1) I_{t} = I_{1} + I_{2} + I_{3}
Từ Định luật Ohm, bạn cũng biết rằng, (2) I_{t} = E/ R_{t}, I_{1} = E/R_{1}, I_{2} = E/R_{2}, I_{3} = E/R_{3}
Bạn có thể thay thế các giá trị từ bốn phương trình (2) vào phương trình (1), điều này sẽ cho ra, (3) E/R_{t} = E/R_{1} + E/R_{1} + E/R_{3}
Bây giờ hãy sử dụng một chút đại số cho phương trình (3), và nhớ rằng bạn có thể làm gần như bất cứ điều gì với một bên của phương trình miễn là bạn làm hoàn toàn giống như với bên kia. Vì vậy, việc chia cả hai bên cho E sẽ cho ra
![]()
Áp dụng công thức này vào mạch song song giả định trước đó với R_{1} = 300 ohm, R_{2} = 200 ohm, và R_{3} = 60 ohm. Thay các giá trị này vào công thức bạn vừa tìm được, bạn sẽ có
![]()
Trước khi bạn cộng các phân số này lại, bạn cần phải làm cho chúng có cùng mẫu số. Trong trường hợp này, mẫu số chung nhỏ nhất là 600; và phương trình của bạn sẽ trở thành
![]()
Hãy nghịch đảo cả hai bên của phương trình, và bạn sẽ thu được (1/R_{t} = 15/600) khi lật ngược chúng.
![]()
Công thức bạn vừa tính có thể mở rộng dễ dàng để tính toán cho bất kỳ số lượng điện trở nào trong một kết hợp song song. Ví dụ, nếu bạn có năm điện trở trong mạch song song của mình, công thức cho tổng điện trở của chúng sẽ là
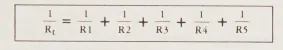
Một công thức đơn giản hóa cho hai điện trở không bằng nhau có thể được tạo ra bằng cách mở rộng công thức, cho bất kỳ số lượng điện trở nào trong mạch song song.
Hãy xem xét một mạch đơn giản như hình minh họa, với một dòng điện chảy qua một cặp điện trở được nối song song, sau đó quay lại nguồn điện. 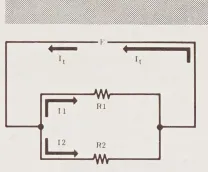
Bạn biết rằng: 1/R_{t} = 1/R_{1} + 1/R_{2}
Công thức toán học đơn giản để tìm số chung nhỏ nhất là: 1/A + 1/B = (B + A) / AB
Sử dụng quy tắc này trong phương trình cho hai điện trở nối song song sẽ cho kết quả như sau: 1/R_{t} = (R_{2} + R_{1}) / (R_{1} x R_{2})
Vì chúng ta đã tìm được một mẫu số chung nhỏ nhất, ta có thể đảo ngược cả hai bên của phương trình thứ ba và thu được: R_{t} = (R_{1} x R_{2}) / R_{1} + R_{2})
Bạn có thể diễn giải công thức trên như sau: Tổng điện trở trong một mạch song song gồm hai điện trở có giá trị không bằng nhau được tính bằng cách nhân giá trị của một điện trở với giá trị của điện trở thứ hai; sau đó cộng giá trị của một điện trở với giá trị của điện trở thứ hai và sau đó chia kết quả đầu tiên cho kết quả thứ hai. Đây là một phương trình hữu ích mà bạn nên biết.
Bây giờ bạn có thể sử dụng công thức này cho mạch song song chứa hai điện trở có giá trị là 60 và 40 ohm mà bạn đang xem xét. Hãy nhớ rằng khi đo bằng ôm kế, tổng điện trở của mạch như vậy là 24 ohm. Hãy xem xét xem liệu công thức có cho kết quả tương tự không.
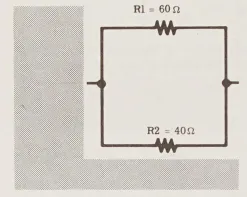
- Nhân hai giá trị của hai điện trở: 60 x 40 = 2400
- Cộng hai giá trị của hai điện trở: 60 + 40 = 100
- Hãy lấy kết quả phép nhân và chia cho tổng hai giá trị: 2400/100 = 24Ω
Vậy bạn thấy rằng giá trị tổng điện trở được tính toán và giá trị được chỉ ra là giống nhau. Bạn có thể tự tin khẳng định rằng việc kết hợp song song của một điện trở 60 ohm và một điện trở 40 ohm luôn tương đương với một điện trở đơn có giá trị là 24 ohm.
Một ví dụ khác
Công thức này thực sự hữu ích, nên hãy xem thêm một ví dụ nữa để làm cho nó rõ ràng hơn trong tâm trí của bạn. Khi hai điện trở, R1 = 120 ohm và R2 = 60 ohm, được kết nối song song, tổng điện trở của chúng là bao nhiêu?
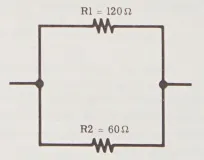
Vẽ sơ đồ mạch và viết ra công thức: R_{t} = (R_{1} x R_{2}) / (R_{1} + R_{2})
Thay các giá trị đã biết vào công thức: R_{t} = (120 x 60) / (120 + 60) = 7200/180 = 40Ω
Tổng điện trở của sự kết hợp song song là 40 ohm, tức là nó sẽ hoạt động như một điện trở đơn có giá trị 40 ohm.
Bạn có thể sử dụng công thức để tìm giá trị của hai điện trở song song để giải quyết các vấn đề phức tạp hơn bằng cách áp dụng công thức nhiều lần để giảm mạch về dạng đơn giản hơn.
Giả sử bạn có ba điện trở nối song song – R1 có giá trị là 300 ohm, R2 có giá trị là 200 ohm và R3 có giá trị là 60 ohm. Bạn muốn biết điện trở hiệu dụng của kết hợp này là bao nhiêu?.
Trước hết, xem xét R1 và R2 một cách độc lập. Thay các giá trị biết vào công thức R_{t} = (R_{1} x R_{2}) / (R_{1} + R_{2}) và bạn sẽ có giá trị của điện trở tương đương của kết hợp R_{1} và R_{2}, mà chúng ta gọi là R_{a} Sau đó kết hợp R_{a} với R_{3}theo cách tương tự và kết quả sẽ là điện trở hiệu dụng (effective resistance) của toàn bộ mạch.
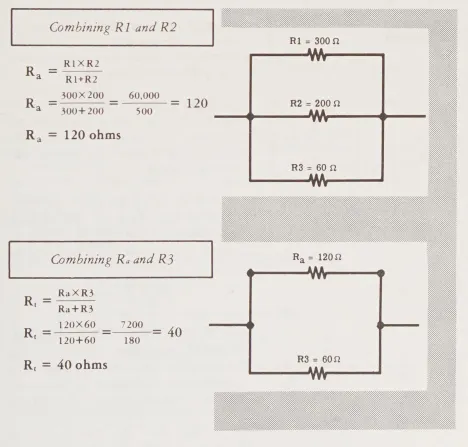
Tổng điện trở của ba điện trở được nối song song là 40 ohm, và kết hợp này sẽ hoạt động như một điện trở đơn có giá trị là 40 ohm trong mạch.
Áp Dụng Định Luật Ohm Trong Mạch Song Song【Applying Ohm’s Law in Parallel Circuits】
Bạn đã thấy cách sử dụng Định luật Ohm trong mạch song song. Trong thực tế, bạn có thể tính được nhiều đại lượng khác nhau như dòng điện, điện áp và điện trở chưa biết trong các mạch như vậy bằng cách áp dụng định luật này.
Nếu bạn muốn tìm điện trở của một điện trở kết nối song song với một hoặc nhiều điện trở khác, bạn cần ngắt kết nối điện trở đó ra khỏi mạch trước khi sử dụng ôm kế. Nếu không, ôm kế sẽ đọc tổng điện trở của toàn bộ tổ hợp (kết hợp) điện trở song song.
Tương tự, nếu bạn muốn đo dòng điện chạy qua một điện trở cụ thể trong một tổ kết hợp các điện trở song song bằng một ampe kế, bạn cũng phải ngắt kết nối và lắp ampe kế vào đúng vị trí để đọc dòng điện chạy qua điện trở đó.
Trong cả hai trường hợp, việc sử dụng Định luật Ohm có thể giúp bạn tiết kiệm thời gian và công sức.
Đối với việc đo điện áp tồn tại trong mạch song song, bạn có thể sử dụng vôn kế trực tiếp mà không cần phải ngắt kết nối. Tuy nhiên, sử dụng Định luật Ohm một cách thông minh cũng có thể cung cấp thông tin bạn cần mà không cần phải đo lường thực tế.
Giải Quyết Các Giá Trị Không Biết Trong Mạch Song Song【Solving Unknowns in Parallel Circuits】
Sáu thông tin đã biết này, tất cả đều đã quen thuộc với bạn, là đủ để tìm ra các giá trị chưa biết trong một mạch song song.
Trong mạch như hìnhminh họa, có một điện áp E được áp dụng qua ba điện trở – R1, R2 và R3 – được kết nối song song. Bạn biết những điều gì về mạch này không?
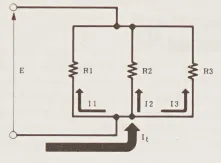
1.Định luật thứ nhất của Kirchhoff nói rằng: I_{t} = I_{1} + I_{2} + I_{3}
2.Bạn biết rằng toàn bộ điện áp mạch (E) xuất hiện qua mỗi trong ba điện trở song song.
3.kết hợp với Định luật Ohm, giúp bạn nhận biết rằng: I_{1} = E/R_{1}, I_{2} = E/R_{2}, I_{3} = E/R_{3}
4.Mọi mạch song song có thể được rút gọn thành một mạch tương đương
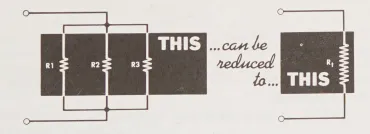
5.Sau đó, Định luật Ohm có thể được áp dụng vào mạch tương đương: I_{t} = E/R_{t} or R_{t} = E/I_{t} or E = I_{t} x R_{t}
6.Tổng điện trở của bất kỳ mạch song song nào có thể được tính bằng cách sử dụng công thức: 1/R_{t} = 1/R_{1} + 1/R_{2} + 1/R_{3} + … và cho 2 điện trở được nối song song R_{t} = (R_{1} x R_{1}) / (R_{1} + R_{2})
Vấn Đề 1
Trong một mạch, có hai điện trở được nối song song. Một trong số chúng có giá trị là 15 ohm, nhưng cái kia không có bất kỳ dấu hiệu nào. Bạn không có ôm kế, nhưng có cả vôn kế và ampe kế. Sử dụng các thiết bị này, bạn đo được rằng điện áp qua tổ hợp song song là 6 volt và dòng điện chảy vào tổ hợp là 1 ampe. Bạn cần biết giá trị của điện trở không được đánh dấu.
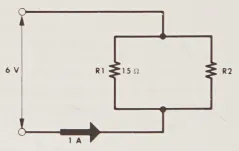
Giải: Đầu tiên, vẽ sơ đồ mạch và điền vào các giá trị bạn biết. Ngay lập tức, bạn thấy mình biết hai trong số ba lượng của Định luật Ohm, và R_{t} = E/I_{t} = 6/1. Do đó, tổng điện trở của mạch song song là 6 ohm.
Bạn đã biết giá trị của R_{1} (nó được đánh dấu 15 ohm). Vậy hãy sử dụng (Công thức Điện trở Song Song), và thay thế các giá trị đã biết ở bất kỳ nơi nào bạn có thể. Do đó, trong trường hợp này:
R_{t} = (R_{1} x R_{2}) / (R_{1} + R_{2})
6 = (15 x R_{2}) / (15 + R_{2})
Bây giờ nhân cả hai bên của phương trình này với hệ số (15 + R2), bạn sẽ được
6 x (15 + R_{2}) = 15 x R_{2}
Nhân đại số bên trái của phương trình: 90 + 6R_{2} = 15R_{2}
Giải phương trình này bằng cách sử dụng các quy tắc đơn giản của đại số, bạn sẽ thấy
15R_{2} – 6R_{2} = 90
9R_{2} = 90
R_{2} = 10 ohm
Vấn Đề 2
Bạn đối diện với một mạch có ba điện trở có giá trị lần lượt là 3, 9 và 12 ohm, được nối song song. Bạn có thể đo được rằng dòng điện chảy qua điện trở 9 ohm là 8 ampe bằng một ampe kế, nhưng hai điện trở còn lại không thể tiếp cận được. Bạn cần biết dòng trong mạch (có thể vì bạn muốn kết nối một tải vào mạch mà sẽ bị cháy nếu dòng điện qua nó quá lớn, và bạn cần tìm giá trị của điện trở mà bạn sẽ phải chèn vào mạch để bảo vệ tải này).
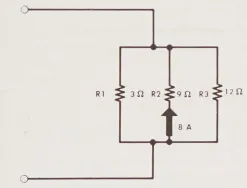
Vẽ sơ đồ mạch và điền vào đó các giá trị bạn biết. Bạn đã biết hai trong số các thông tin cần thiết về R2, hãy sử dụng Định luật Ohm để tính toán thông tin thứ ba:
E = I_{2} x R_{2} = 9 ohm x 8 ampe = 72v
Điện áp qua một nhánh của mạch song song là điện áp qua tất cả các nhánh khác; vì vậy, bạn đã có đủ thông tin cần để biết về R1 và R3 để sử dụng Định luật Ohm và tìm ra dòng điện chảy qua từng nhánh của chúng.
Bắt đầu với R1. Bạn biết rằng giá trị của nó là 3 ohm, và điện áp qua nó là 72 volt. Do đó: I_{1} = E / R_{1} = 72 / 3 = 24 ampe
Sau đó, xử lý R3. Nó có giá trị là 12 ohm, và điện áp qua nó vẫn là 72 volt. Điều này có nghĩa là: I_{3} = E / R_{3} = 72 / 12 = 6 ampe
Bạn đã biết dòng điện chảy qua tất cả ba nhánh của mạch song song. Theo Định luật thứ hai của Kirchhoff, tổng dòng của mạch chính bằng tổng của ba dòng này (I_{t} = I_{1} + I_{2} +I_{3}). Do đó, trong trường hợp này: I_{t} = 8 + 24 + 6 = 38 ampe
đó là giá trị của dòng mạch mà bạn đang tìm
Thí Nghiệm/Ứng Dụng – Định luật Ohm Và Điện Trở Trong Mạch Song Song【Experiment/Application-Ohm’s Law and Parallel Resistances】
Để xem cách sử dụng ampe kế và vôn kế thay thế cho ôm kế để tìm giá trị của điện trở riêng lẻ và điện trở tổng trong sự kết hợp song song, bốn pin khô có thể được mắc nối tiếp để sử dụng làm nguồn điện áp. Sau đó nối vôn kế qua pin khô để đảm bảo điện áp không đổi ở mức 6 volt và nối ampe kế nối tiếp với cực âm (-) của pin để đo đọc dòng điện.
Bây giờ, nếu bạn nối một cầu chì, một điện trở có một dải màu cam và hai dải màu đen, và một công tắc nối tiếp giữa cực dương (+) của ampe kế và pin, bạn sẽ thấy điện áp vẫn ở mức 6 volt, và điều đó dòng điện chỉ ra là 0,2 ampe. Theo Định luật Ohm, giá trị điện trở phải là 30 ohm và việc kiểm tra mã màu cho thấy đây thực sự là giá trị chính xác.
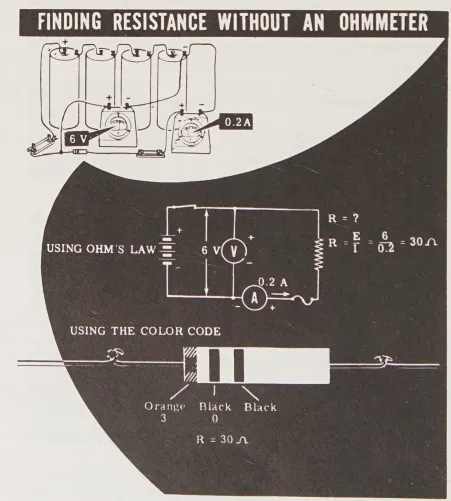
Nếu thêm một điện trở khác, có màu nâu, xanh lá cây và đen, vào mạch nối song song, bạn sẽ thấy rằng dòng điện đọc được là 0,6 ampere, không có thay đổi trong điện áp. Vì điện trở đầu tiên truyền qua 0,2 ampere, nên dòng điện qua điện trở thứ hai phải là 0,4 ampere. Vậy, theo Định luật Ohm, giá trị của điện trở thứ hai là 6 volt chia cho 0,4 ampere, tức là 15 ohm.
Tổng điện trở, của sự kết hợp song song là 6 volt chia cho tổng dòng điện, tức là 0,6 ampere, hoặc 10 ohm.
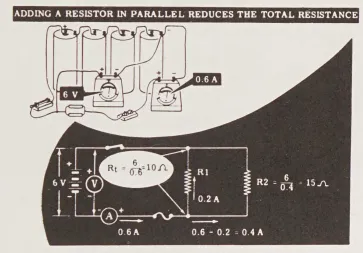
Khi thêm một điện trở khác (một dải màu cam và hai dải màu đen) vào song song, bạn thấy dòng điện tăng thêm 0,2 ampere – cho thấy điện trở được thêm vào có giá trị là 30 ohm theo Định luật Ohm. Tổng dòng điện hiện là 0,8 ampere, dẫn đến tổng điện trở là 7,5 ohm cho sự kết hợp song song.
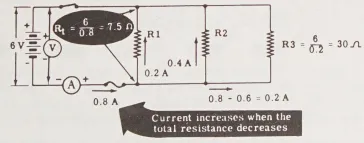
Sau khi bạn đã tách (ngắt kết nối) pin và các điện trở, bạn có thể sử dụng ôm kế để kiểm tra tổng và từng điện trở riêng lẻ; bạn sẽ thấy rằng các giá trị từ Định luật Ohm và mã màu hoàn toàn trùng khớp với những giá trị được đo bằng ôm kế.
Thí Nghiệm/Ứng Dụng – Định luật Ohm Và Dòng Điện Trong Mạch Song Song【Experiment/Application-Ohm’s Law and Parallel Circuit Current】
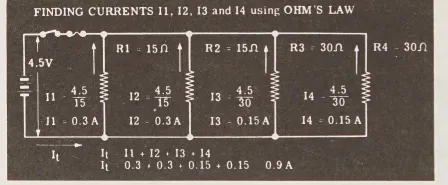
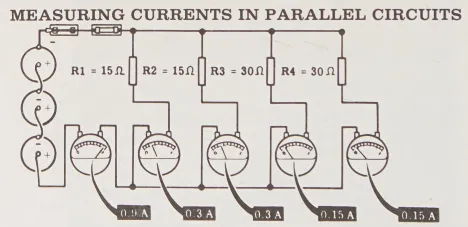
Chỉ cần sử dụng ba viên pin được kết nối nối tiếp như nguồn điện, bạn có thể nối vôn kế qua các viên pin đó. Sau đó, bạn có thể kết nối bốn điện trở – hai điện trở 15 ohm và hai điện trở 30 ohm – song song qua các viên pin.
Theo Định luật Ohm, dòng điện qua mỗi điện trở 15 ohm sẽ là 0,3 ampere, và qua mỗi điện trở 30 ohm sẽ là 0,15 ampere. Tổng dòng điện sẽ là tổng của các dòng điện qua từng điện trở riêng lẻ, tức là 0,9 ampere.
Tóm Tắt Đánh Giá Lại Về Mạch Song Song【Review of Parallel Circuits】
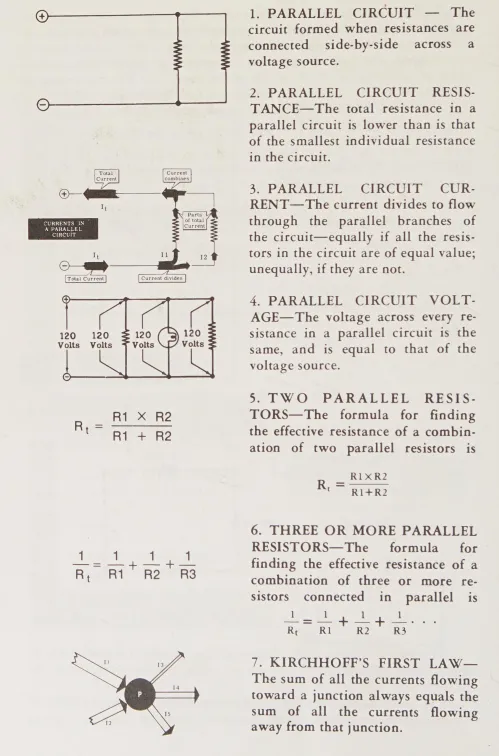
- Mạch song song (PARALLEL CIRCUIT) – Mạch được tạo ra khi các điện trở được kết nối song song với nguồn điện áp
- Điện trở mạch song song (PARALLEL CIRCUIT RESISTANCE) – Trong mạch song song, tổng điện trở, thấp hơn so với điện trở riêng lẻ nhỏ nhất trong mạch
- Dòng điện trong mạch song song (PARALLEL CIRCUIT CURRENT) – Dòng điện trong mạch song song phân chia để chảy qua các nhánh song song của mạch – đồng đều nếu tất cả các điện trở trong mạch có cùng giá trị; không đồng đều nếu chúng không giống nhau
- Điện áp trong mạch song song (PARALLEL CIRCUIT VOLTAGE) – Điện áp qua mỗi điện trở trong mạch song song đều giống nhau và bằng với nguồn điện áp
- Hai điện trở mắc song song (TWO PARALLEL RESISTORS) – Công thức để tính điện trở hiệu dụng của hai điện trở mắc song song là: R_{t} = (R_{1} x R_{2}) / (R_{1} + R_{2})
- Ba hoặc nhiều hơn ba điện trở mắc song song (THREE OR MORE PARALLEL RESISTORS) – Công thức để tính điện trở hiệu dụng của một kết hợp ba hoặc nhiều hơn ba điện trở mắc song song là: 1/R_{t} = 1/R_{1} + 1/R_{2} + 1/R_{3}…
- Định luật đầu tiên của Kirchhoff (KIRCHHOFF’S FIRST LAW) -Tổng của tất cả các dòng điện chảy vào một nút, luôn bằng tổng của tất cả các dòng điện chảy ra khỏi nút đó
Tóm Tắt Đánh Giá Lại Về Định Luật Ohm Và mạch Song Song【Review of Ohm’s Law and Parallel Circuits】
Nếu một mạch bao gồm hai hoặc nhiều điện trở- R_{1}, R_{2}, R_{3}, v.v. mắc song song, thì áp dụng các quy tắc sau để sử dụng Định luật Ohm:
R_{t}, I_{t} và E được sử dụng cùng nhau.
R_{1}, I_{1} và E được sử dụng cùng nhau.
R_{2}, I_{2} và E được sử dụng cùng nhau; và tiếp tục như vậy.
Chỉ sử dụng các đại lượng có chỉ số giống nhau hoặc không có chỉ số nào, để tìm một giá trị chưa biết thông qua Định luật Ohm.
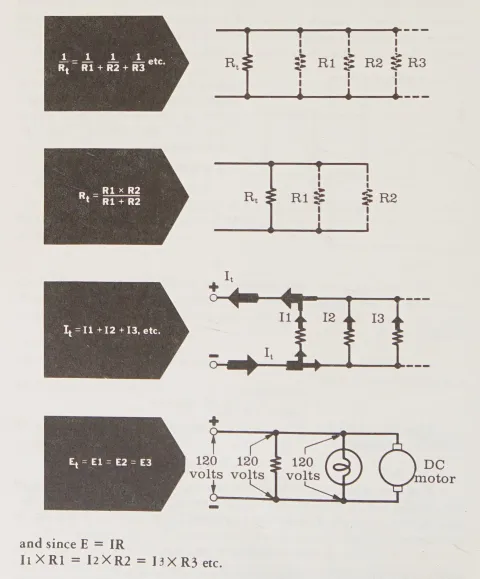
Và vì E = I x R, nên I_{1} x R_{1} = I_{2} x R_{2} = I_{3} x R_{3} vv.
